A New Elliptic Curve Based Analogue of Rsa

refer: A New Elliptic Curve Based Analogue of RSA

椭圆曲线

令 p 和 q 是素数，都大于3。并且满足$4a^3 + 27b^2 \not\equiv 0 \pmod{p}$。用$E_p(a, b)$表示模p参数为a,b的椭圆曲线。$y^2 \equiv x^3 + ax + b \pmod{p}$。

椭圆曲线的加法计算定义为

$$ P+Q=R \tag 1 $$

设$P=(x_1, y_1)，Q=(x_2,y_2)，R=(x_3, y_3)$

$$ x3 \equiv \lambda^2-x_1-x_2 \mod{p} \tag 2 $$

$$ y_3\equiv \lambda(x_1-x_3) - y_1 \pmod{p} $$

$$ \lambda \equiv \begin{cases} \frac{y_1-y_2}{x_1-x_2} & if x_1 \not\equiv x_2 \pmod{p} \\ \\ \frac{3x_1^2 + a}{2y_1} & ifx1=x2 \pmod{p} \end{cases} $$

椭圆曲线的阶表示为

$$ |E_p(a, b)| = 1 + \sum_{x=1}^p((\frac{z}{p}) + 1) $$

$(\frac{z}{p})$是椭圆曲线的勒让德符号，$z\equiv x^3 + ax + b\pmod{p}$。勒让德符号的值为1, 0, -1。

很容易证明：

(1) y有两个值对于一个x，当z是关于p的一个二次剩余

(2) y 有一个值对于一个x，当$z \equiv 0 \pmod{p}$

(3) y 不存在对于一个x， 当z是关于p的一个二次非剩余

对一个很大的p使用这个方法显然是不够有效的。更加有效的计算椭圆曲线的阶的算法是Schoof’s algorithm，在 维基百科 中也介绍了很多算法，但这篇主要是介绍A New Elliptic Curve Based Analogue of RSA这个密码系统就不多描述了。

一个很重要的定理是Hasses 定理。令$E$是定义在$F_p$上的椭圆曲线，$E$上的点的数量也就是$E$的阶满足

$$ |p+1-#E(F_p)| \leq 2 \sqrt{q} $$

其中$#E(F_p)$表示椭圆曲线$E$的阶。有了Hasses定理，可以定义

$$ |E_p(a,b)|=p+1+\alpha, \quad where\ |\alpha| \leq 2\sqrt{p} $$

椭圆曲线的互补群

令p是一个素数，a, b是椭圆曲线$E_p(a, b)$的参数。用$E_p(a,b)$来表示满足

$$ y^2\equiv x^3+ax+b $$

的所有整数对$(x,y)$，但y是非负整数。即y可以表示成

$$ y\equiv u\sqrt{v} \pmod{p} $$

u是一个非负整数，v是模p的一个二次非剩余定值。比如有$(x_1, y_1)=(x_1, u_1\sqrt{v})$，

$(x_2, y_2)=(x_2,u_2\sqrt{v})$。

互补群的阶被这样给出

$$ |\overline{E_p(a,b)}|=1+\sum_{x=1}^p(1-(\frac{z}{p})) $$

运用Hasses定理

$$ |\overline{E_p(a,b)}|=p+1-\alpha $$

加密解密

选择两个素数p, q。令n=pq。在$Z_n$上选择一个椭圆曲线。椭圆曲线的参数满足

$$ \gcd(4a^3+27b^2, n)=1 $$

令

$$ |E_p(a,b)|=p+1+\alpha，|\overline{E_p(a,b)}|=p+1-\alpha \\ |E_q(a,b)|=p+1+\beta，|\overline{E_q(a,b)}|=p+1-\beta $$

将明文编码成坐标(x, y)的横坐标x。$y\equiv \sqrt{x^3+ax+b} \pmod{n}$ ，注意开根是在模n的意义下开根。

加密表示为

$$ (s,t)\equiv (x,y)*e \pmod{n} $$

s为密文。

解密表示为i

$$ (x,y)\equiv (s, t)*d_i \pmod{n} $$

其中e和d的选择

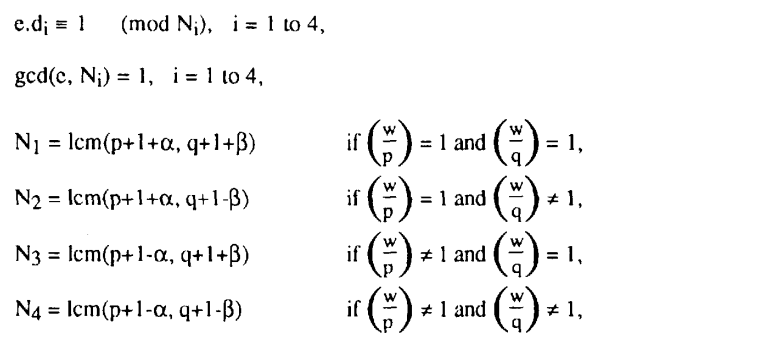
$$ w\equiv s^3+as+b \pmod{n} $$

但这篇论文很奇怪的地方在，如果要确定e，那么要知道N，N是从w的值来决定是那种情况，可是还没加密呢，哪来的s，哪来的w？后来查阅资料找到了另一种确定e的方法

这里就非常的清楚$gcd(e, (p^2-tp^2)(q^2-tq^2))=1$。$t_p=-\alpha,t_q=-\beta$

虽然是椭圆曲线问题，但是此密码的安全性仍然是基于大整数分解和计算椭圆曲线阶的难题。与RSA相似。

Example

from sage.all import *
from sage.all_cmdline import *
from Crypto.Util.number import *
from sympy import nthroot_mod

Nbits = 256

plaintext = bytes_to_long(b"hello world")

def gen_pubkey(p, q):
    n = p*q

    a = getRandomInteger(Nbits // 2)
    b = getRandomInteger(Nbits // 2)

    assert gcd(4*a**3 + 27*b**2, n) == 1
    
    e = getPrime(256)
    orderp = EllipticCurve(GF(p), [a, b]).order()
    orderq = EllipticCurve(GF(q), [a, b]).order()
    tp = p + 1 - orderp
    tq = q + 1 - orderq
    assert gcd(e, (p**2 - tp**2)*(q**2 - tq**2))

    public_key = (n, a, b, e)
	
    return public_key

def gen_prikey(cipher, p, q, a, b, tp, tq):
    cx = cipher[0]
    u = cx**3 + a*cx + b % n
    up = legendre_symbol(u, p)
    uq = legendre_symbol(u, q)
    assert up == uq == 1
    d = inverse_mod(e, lcm(p+1-tp, q+1-tq))

    return d

p, q = getPrime(Nbits), getPrime(Nbits)
n, a, b, e = gen_pubkey(256)
ciphertext = e * plaintext

print("public key:")
print(f"n = {n}\na = {a}\nb = {b}\ne = {e}")
print("cipher:")
print(ciphertext)

orderp = EllipticCurve(GF(p), [a, b]).order()
orderq = EllipticCurve(GF(q), [a, b]).order()
tp = p + 1 - orderp
tq = q + 1 - orderq

d = gen_prikey(ciphertext, p, q, a, b, tp, tq)

m = d * ciphertext
print(long_to_bytes(int(m[0])))