Elliptic Curve
定义
在数学上,椭圆曲线(Elliptic curve,缩写为EC)为一平面代数曲线,由如下形式的方程定义 $$ y^2=x^3 + ax + b $$
其中$a$和$b$为实数。这类方程被称为short Weierstrass (韦尔斯特拉斯)方程。椭圆曲线的定义也要求曲线是非奇异的。几何上来说,这意味着图像里面没有尖点、自相交或孤立点。代数上来说,这成立当且仅当判别式 $$ \Delta=-16(4a^3+27b^2) $$ 不等于0。 有short Weierstrass自然也有long Weierstrass方程 $$ y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6 $$ (至于为什么没有$a_5$我也不知道,看过的资料里都是没有$a_5$的) long Weierstrass形式可以转化为short Weierstrass形式。 令$y\longrightarrow y-\frac{(a_1x+a_3)}{2}$,化简后 $$ y^2=x^3+Ax^2+Bx+C $$ 再令$x\longrightarrow x-\frac{A}{3}$ $$ y^2=x^3+ax+b $$
实数域
椭圆曲线的加法
由椭圆曲线的加法定义:两个点的连线交曲线的第三点并取与x轴的对称点。 如计算$P=(X_p, Y_p)$和$Q=(X_Q, Y_Q)$的和$R=(X_R, Y_R)$ $$ \lambda=\frac{Y_Q-Y_P}{X_Q-X_P} $$ $$ X_R=\lambda^2-X_P-X_Q $$ $$ Y_R=\lambda(X_P-X_R)-Y_P $$ 或 $$ Y_R=\lambda(X_Q-X_R)-Y_Q $$
当$P=Q$的时候,$P,Q$的连线变成椭圆曲线的切线。此时对曲线方程的两边取微分,并且知道切线的斜率等于y的微分比x的微分 $$ 2yd_y=3x^2d_x+ad_x $$ 整理后得 $$ \lambda=\frac{d_y}{d_x}=\frac{3x^2+a}{2y} $$ 计算$X_R,Y_R$的公式与上面相同。
有限域
实际上在定义在有限域上的椭圆曲线的加法也可以用实数域的公式,只不过除法变成求逆元 $$ \lambda=(Y_Q-Y_P)(X_Q-X_P)^{-1} \pmod{p} $$ 当$P=Q$时 $$ \lambda=(3x^2+a)(2y)^{-1} \pmod{p} $$ 但是计算乘法逆元总是复杂的(即使用拓展欧几里德算法)。所以介绍下射影平面坐标。
射影坐标
以上所讲的Weierstrass方程是仿射平面下的形式。仿射坐标到射影坐标的转换就是 $$ (X, Y) \longrightarrow (X,Y,Z) $$ 从射影坐标到仿射坐标的转换 $$ (X,Y,Z)(X, Y) \longrightarrow (X,Y,Z)(\frac{X}{Z},\frac{Y}{Z}) $$ 于是得到椭圆曲线射影坐标的形式 $$ Y^2Z=X^3+aXZ^2+bZ^3 $$ 无穷远点在数学上也是由射影平面来的。用坐标来表达就是$Z=0$的点。对于上面的方程来说就是$(0:Y:0)$。一般来说会使用点$(0:1:0)$来表示无穷远点。比如sagemath。
雅可比坐标
从仿射坐标到雅可比坐标 $$ (x, y)\longrightarrow(X:Y:Z) $$ 从雅可比坐标到仿射坐标 $$ (X:Y:Z)\longrightarrow(X/Z^2,Y/Z^3) $$ 由此可见$(\lambda^2X:\lambda^3Y:\lambda Z)$对于非零的$\lambda$表示的是同一个点。
雅可比坐标的加法
这里就不用公式了,直接用sagemath吧
sage: from Crypto.Util.number import getPrime
sage: p = getPrime(128)
sage: p
301106202796104772606281479390414064437
sage: E = EllipticCurve(GF(p), [0, 7])
sage: E
Elliptic Curve defined by y^2 = x^3 + 7 over Finite Field of size 301106202796104772606281479390414064437
sage: P = E.lift_x(1234)
sage: P
(1234 : 151759733218367662729854605113112589945 : 1)
sage: Q = E.lift_x(4321)
sage: Q
(4321 : 20096162093032149077296625270192771385 : 1)
sage: P+Q
(297720150792495705916131422544224381584 : 267287806774622770961153728731746702305 : 1)
sage: X1, Y1, Z1 = P
sage: X2, Y2, Z2 = Q
sage: I1 = Z1^2; I2=Z2^2
sage: J1=I1*Z1
sage: J2=I2*Z2
sage: U1=X1*I2
sage: U2=X2*I1
sage: H=U1-U2
sage: F=4*H^2
sage: K1=Y1*J2; K2=Y2*J1
sage: R=2*(K1-K2)
sage: G = F*H
sage: V = U1*F
sage: X3 = R^2 + G -2*V; Y3=R*(V-X3)-2*K1*G; Z3=((Z1+Z2)^2-I1-I2)*H
sage: (X3, Y3, Z3)
(214535640891103999239269350061448120807,
240487449847258905205618475831905609624,
301106202796104772606281479390414058263)
sage: X3 *= inverse_mod(Z3, p)^2
sage: Y3*= inverse_mod(Z3, p)^3
sage: X3, Y3
(297720150792495705916131422544224381584,
267287806774622770961153728731746702305)
雅可比坐标的倍点
同样直接用sagemath来表示,曲线的参数和P点与上面相同。
sage: N = Z1^2
sage: E = Y1^2
sage: B = X1^2
sage: L = E^2
sage: S = 2*((X1 + E)^2 - B - L)
sage: M= 3*B + 0*N^2
sage: X2 = M^2 - 2*S
sage: Y2 = M*(S-X2) - 8*L
sage: Z2 = (Y1+Z1)^2-E-N
sage: (X2, Y2, Z2)
(2318785766432, 3530945306848783384, 2413263640630552853427730835811115453)
sage: X2 *= inverse_mod(Z2, p)^2
sage: Y2 *= inverse_mod(Z2, p)^3
sage: Z2 *= inverse_mod(Z2, p)
sage: (X2, Y2, Z2)
(211487819687729717989558216870258642315,
181567709617916269765770514916557993658,
1)
sage: 2*P
(211487819687729717989558216870258642315 : 181567709617916269765770514916557993658 : 1)
解释一下这句M = 3*B + 0*N^2,原先的公式是 $$ M=3B+aN^2 $$ $a$就是曲线的参数a,上面的曲线为 $$ y^2=x^3+7 \quad(a=0,b=7) $$ 更多的细节可以看论文。
Twisted Edwards curve
定义
–
twisted Edwards curve也是定义在仿射平面上,形如 $$ ax^2+y^2=1+dx^2y^2 $$
twisted Edwards curve上的加法
$$ \left(x_{1}, y_{1}\right)+\left(x_{2}, y_{2}\right)=\left(\frac{x_{1} y_{2}+y_{1} x_{2}}{1+d x_{1} x_{2} y_{1} y_{2}}, \frac{y_{1} y_{2}-a x_{1} x_{2}}{1-d x_{1} x_{2} y_{1} y_{2}}\right) $$
twisted Edwards curve上的倍点
$$ 2(x_1,y_1)=\left(\frac{2x_{1}y_{1}}{ax_{1}^2+y_{1}^{2}}, \frac{y_{1}^2- a x_{1}^{2}}{2-a x_{1}^2- y_{1}^2}\right) $$
射影坐标
与Weierstrass curve一样
$$ (X:Y:Z)\longrightarrow \left(\frac{X}{Z},\frac{Y}{Z}\right) $$ 于是得到射影平面的形式
$$ (aX^2+Y^2)Z^2=Z^4+dX^2Y^2 $$ 加法
计算$(X_1:Y_1:Z_1)+(X_2:Y_2:Z_2)=(X_3:Y_3:Z_3)$ $$ \begin{array}{l} A=Z_{1} \cdot Z_{2} \\ B=A^{2} \\ C=X_{1} \cdot X_{2} \\ D=Y_{1} \cdot Y_{2} \\ E=d C \cdot D \\ F=B-E \\ G=B+E \\ X_{3}=A \cdot F\left(\left(X_{1}+Y_{1}\right) \cdot\left(X_{2}+Y_{2}\right)-C-D\right) \\ Y_{3}=A \cdot G \cdot(D-a C) \\ Z_{3}=F \cdot G \end{array} $$ 倍点
计算$(X_3:Y_3:Z_3)=2(X_1:Y_1:Z_1)$
$$ \begin{array}{l} B=\left(X_{1}+Y_{1}\right)^{2} \\ C=X_{1}{ }^{2} \\ D=Y_{1}{ }^{2} \\ E=a C \\ F=E+D \\ H=Z_{1}{ }^{2} \\ J=F-2 H \\ X_{3}=(B-C-D) \cdot J \\ Y_{3}=F \cdot(E-D) \\ Z_{3}=F \cdot J \end{array} $$
Montgomery Curves and Twisted Edwards Curves
扭曲爱德华曲线在域$\displaystyle{K}$上双有理等价于蒙哥马利曲线,证明可以看论文。这里只是把论文中用sagemath的部分重新贴一下。
sage: R.<a,d,x,y>=QQ[]
sage: A=2*(a+d)/(a-d)
sage: B=4/(a-d)
sage: S=R.quotient(a*x^2+y^2-(1+d*x^2*y^2))
sage: u=(1+y)/(1-y)
sage: v=(1+y)/((1-y)*x)
sage: 0==S((B*v^2-u^3-A*u^2-u).numerator())
True
所以可以把扭曲爱德华曲线和蒙哥马利曲线进行互相转化。转化的过程可以看wiki
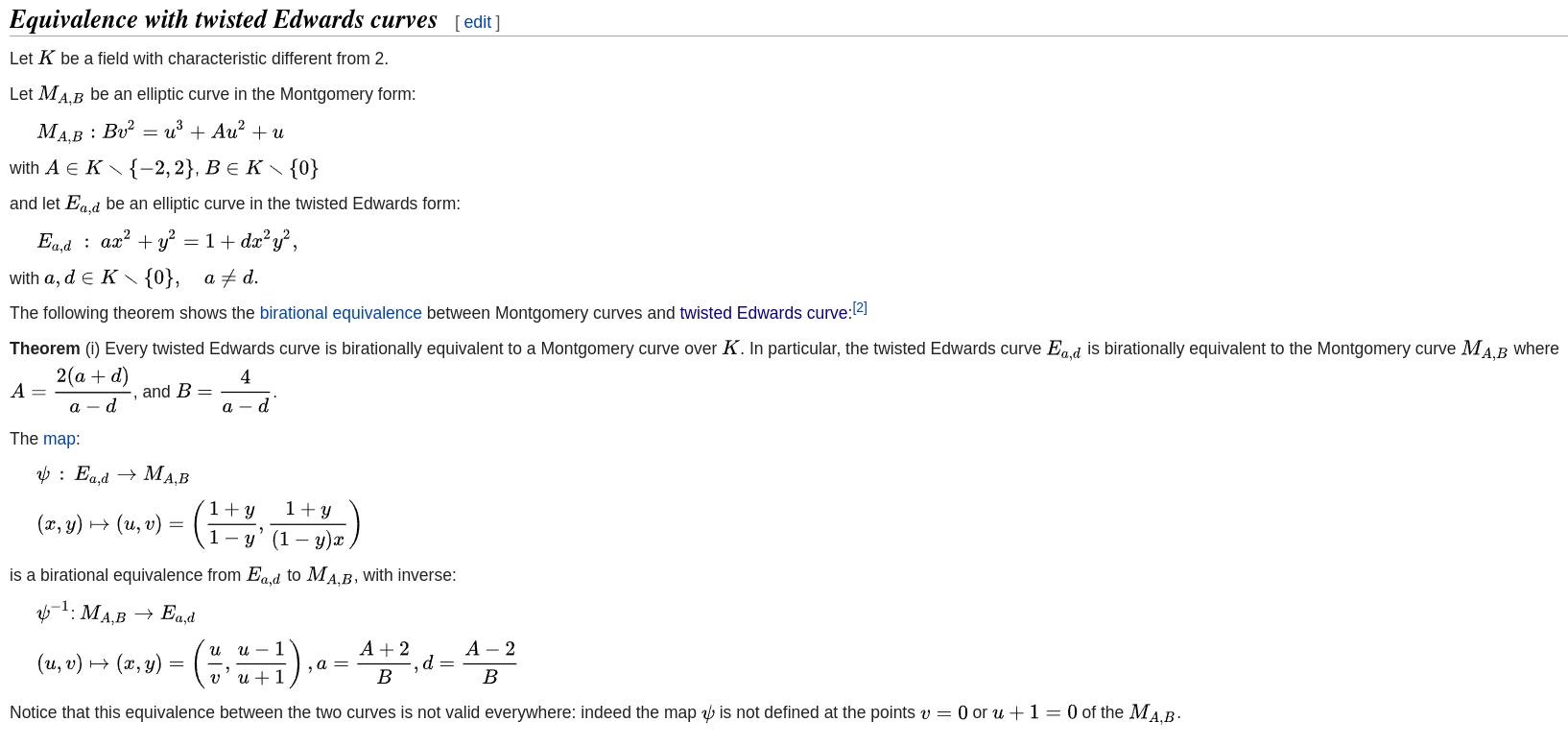
同时蒙哥马利曲线又可以与维尔斯特拉斯方程进行互相转化。

写了一个小demo:
from sage.all import *
def twisted_to_Montgomery(x, y, a, d, p):
"""The map for twisted Edwards curves point to Montgomery curves point
x, y: twisted Edwards curves point
a, d: twisted Edwards curves sach that a*x^2 + y^2 = 1 + d*x^2*y^2
P: The field K(p)
Return: mapped point (u, v) and the Montgomery curves parmteres (A, B)
"""
A = 2*(a + d) * inverse_mod(a-d, p) % p
B = 4 * inverse_mod(a-d, p)
u = (1+y) * inverse_mod((1-y), p) % p
v = u * inverse_mod(x, p)
assert B*v**2 % p == (u**3 + A*u**2 + u) % p; "Error"
return u, v, A, B
def Montgomery_to_Weierstrass(x, y, A, B, p):
"""The map from Montgomery curves point to Weierstrass curves point
x, y: Montgomery curves point
A, B: Montgomery curves sach that B*v^2 = u^3 + A*u^2 + u
P: The field K(p)
"""
a = (3 - A**2) * inverse_mod(3*B**2, p) % p
b = (2*A**3 - 9*A) * inverse_mod(27*B**3, p) % p
t = (3*x + A) * inverse_mod(3*B, p) % p
v = y * inverse_mod(B, p) % p
assert v**2 % p == (t**3 + a*t + b) % p; "Error"
return t, v, a, b
def twisted_to_Weierstrass(x, y, a, d, p):
"""The map for twisted Edwards curves point to Weierstrass curves point
x, y: twisted Edwards curves point
a, d: twisted Edwards curves sach that a*x^2 + y^2 = 1 + d*x^2*y^2
P: The field K(p)
Return: mapped point (t, v) and the Weierstrass curves parmteres (a, b)
"""
u, v, A, B = twisted_to_Montgomery(x, y, a, d, p)
return Montgomery_to_Weierstrass(u, v, A, B, p)
ECDLP
定义
–
椭圆曲线密码学(ECC)依赖于椭圆曲线离散对数问题(ECDLP)的困难。对于两个点$P,Q$,有
$$ Q=l*P $$ 计算$l$,这个问题称为ECDLP。或者记作$log_PQ$。ECDLP本身是十分困难的,但是椭圆曲线参数的选择会降低ECDLP的困难度。下面介绍两个Weak Elliptic Curve。
Pohlig-Hellman Attack
假设我们现在有一个曲线$E(p): y^2=x^3+ax+b$,以及曲线上的两个点$P,Q$且满足$Q=k*P$。点$P$的阶为$n=#$。Pohlig-Hellman Attack的主要思想是把原先在阶为$n$下的ECDLP转化为若干个在$P$的子群下的ECDLP,最后用中国剩余定理恢复在模$n$下的$k$。这种算法在$n$是光滑数是尤其有效。
Sage中的discrete_log方法使用的就是Pohilg-Hellman Attack算法。
sage: m = 21345332
sage: p = 4516284508517
sage: E = EllipticCurve(GF(p), [7,1])
sage: Q = E.gens()[0]
sage: mQ = m*Q
sage: print(E.order().factor())
11 * 13 * 31582419389
sage: time mRec = discrete_log(mQ, Q, operation='+'); mRec
CPU times: user 5.13 s, sys: 23.6 ms, total: 5.16 s
Wall time: 5.16 s
21345332
Smart’s Attack
Smart’s Attack 适用于$#F(p)=p$的曲线。 脚本可以参考这个smart’s attack。