关于Lattice问题的复习和Kannan’s Embedding for solve LWE的学习记录
SVP #
SVP(shortset vector problem)是找到一个格$L$上的最短向量,最短指的是Euclidean Norm(欧几里得范式)最小。一个格中最少有两个具有相同范式的最短向量,并且这两个向量的符号相反,也就是反向。把第一最短向量记为$\lambda_{1}(L)$,第二最短向量为$\lambda_2(L)$。
uSVP #
uSVP(unique SVP)是指在一个格中,满足$\lambda_1(L) \ll \lambda_2(L)$,找到$\lambda_1(L)$。或者给一个辅助变量$\gamma$,$\gamma\lambda_1(L) < \lambda_2(L)$,uSVP就变成$\gamma$-uSVP,$\gamma$可以看作是$\lambda_1(L)$和$\lambda_2(L)$之间的gap。所以$\gamma$-uSVP也可以当作是gapSVP。$\gamma$越大,在这个格$L$中就越容易找到$\lambda_1(L)$。
CVP #
CVP(closest vector problem)是给定一个格$L$和一个不在$L$中的目标向量$t$,在$L$中找到一个向量$v$,与$t$的距离最短。
BDD #
BDD(Bounded Distance Decoding)是在CVP中规定$||v-t|| < \beta\lambda_1(L)$,而且$\beta$小于0.5,找到的$v$一定是唯一的。
LWE #
有一个矩阵$A\in\mathbb{Z}_q^{m\times n}$,一个secret vector $s\in\mathbb{Z}_q^n$,还有一个误差向量 $e\in\mathbb{Z}_q^m$,已知$(A,b=As+e)$,求secret vector $s$。$n$ 称为LWE问题的维数,$m$ 称为LWE问题的样本数(simple number)。
q-ary Lattice #
q-ary Lattice 其实就是把一个$\mathbb{Z}_q$的矩阵转换成$\mathbb{Z}$上的格。比如一个$A\in\mathbb{Z}_q^{m\times n}$,$A$ 的q-ary Lattice就是 $$ L_{(\mathbf{A}, q)}=\left{\mathbf{y} \in \mathbb{Z}_{q}^{m} \mid \mathbf{y} \equiv \mathbf{A} \mathbf{x}(\bmod q) \text { for some } \mathbf{x} \in \mathbb{Z}^{n}\right} $$ $L_{(A,q)}$的基$B$,表示为 $$ \mathbf{B}=\left(\frac{\mathbf{A}^{T}}{q \mathbf{I}_{m}}\right) \in \mathbb{Z}^{(m+n) \times m} $$ 简单证明一下, $$ Ax\equiv b\pmod{q} \\ Ax +kq = b \\ [x_0, x_1,\cdots,x_n| k_0,k_1,\cdots,k_m] \begin{bmatrix} A^{T}\\qI_m \end{bmatrix} = [b_0,b_1,\cdots,b_m] $$
From LWE to BDD #
在LWE问题中,由于error vector $e$很小,所以可以把LWE看成在格$L_{(\mathbf{A}, q)}$上寻找到与目标向量$b$距离最近的向量$s$。并且距离限制为$||e||$。
Kannan’s Embedding #
使用Kannan’s Embedding来解决LWE。实际上Embedding是一个将CVP转化为SVP的方法,在上一节中已经把LWE转化为了BDD问题(BDD就是一种CVP),再使用Embedding的方法把BDD问题化为SVP甚至是uSVP问题(实际上一定可以化为uSVP,只是$\gamma$大不大的问题罢了)。
假设有一个LWE实例$(A,b=As+e)$在$Z_q$上,首先要把$A\in Z_q$转成$B\in\mathbb{Z}$
$$ \mathbf{B}=\left(\frac{\mathbf{A}^{T}}{q \mathbf{I}_{m}}\right) \in \mathbb{Z}^{(m+n) \times m} $$ 将$B$化为标准型矩阵,也就是行阶梯型矩阵$B_{HNF}$,对于所有的$B$,它的行阶梯型矩阵都应该拥有这样的格式 $$ \mathbf{B}_{\mathrm{HNF}}=\begin{pmatrix}\mathbf{I}_{n}\quad\mathbf{A}^{\prime}_{n\times(m-n)}\\ \mathbf{0}\quad q\mathbf{I}_{m-n}\end{pmatrix}\in\mathbb{Z}^{m\times m} $$ 这个应该有严谨的证明过程的,但是我没证出来,就当作是定理好了。这里的$B_{HNF}$已经把全零的行去掉了。
因为从$B$到$B_{HNF}$的变换是线性的,也就是有一个线性变化$P$,使得$B_{HNF}=BP$,如果不能理解的话,可以再复习一下线性代数(所有的线性变化都可以由一个变化矩阵来表示)。那么对$s$做相应的反变换得到$u=P^{-1}s$,依然可以得到 $$ b=B\cdot s+e=B_{HNF}P^{-1}\cdot Pu + e=B_{HNF}\cdot u + e $$
然后就是Embedding,把目标向量嵌入(embedding)到格中,这样就把CVP问题转成SVP问题。 $$ \mathbf{B}^{\prime}=\begin{pmatrix}\mathbf{B_{HNF}}\quad\mathbf{0}\\ \mathbf{b}\quad M\end{pmatrix}\in\mathbb{Z}^{m\times m} $$ $M$ 称作embedding factor,$M$的大小直接影响$\gamma$-uSVP中$\gamma$的大小。在以$B^{\prime}$为基的格中存在 $$ \mathbf{w}=\mathbf{B}^{\prime}\begin{pmatrix} u\\ -1 \end{pmatrix}= \begin{pmatrix} e\\M \end{pmatrix} $$ $\mathbf{w}$这个向量足够小,可以使用BKZ或者LLL规约出来。整个算法的过程如下

我在写的时候把原论文的$B_{HNF}$做了一个转置,因为行阶梯型处理起来会更加舒服(实际上是一样的),而且SageMath中就有内置的化为行阶梯型的方法,在代码里更方便。
How to Choose M #
在原论文中,作者发现随着M的增大,算法所用的时间会变久。
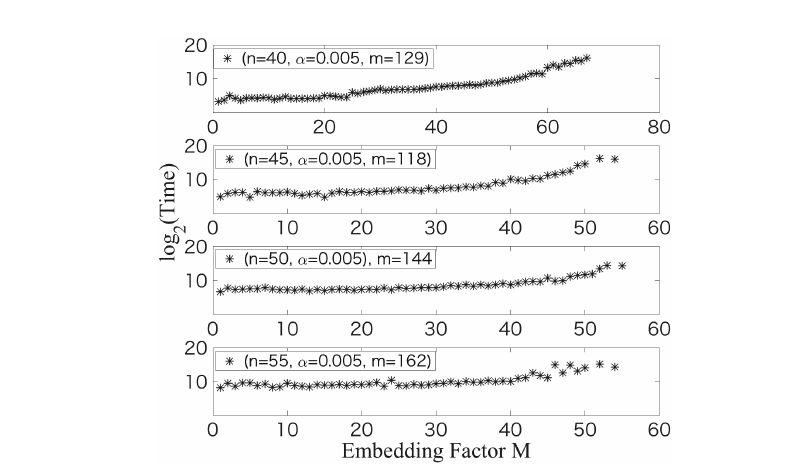
但是太小的M又会导致$w$不是格中最短的向量。最后的结论就是M的大小接近1是最好的选择,如果得不到正确答案,就从1慢慢往上加好了。
参考文献
https://link.springer.com/chapter/10.1007/978-3-319-89500-0_47